生物信息学
序列比对
桂松涛 Blog
songtaogui@163.com

2025年09月
框架
序列比对相关概念
序列比对打分方法
双序列比对算法
多序列比对
生物信息学
序列比对: 1. 相关概念
桂松涛 Blog
songtaogui@163.com

2025年09月
1. 序列比对相关概念
|
AGCACACA | | ACACACTA |
AGCACAC-A | ||||| | A-CACACTA |
AGCACACA--- ||||| ---ACACACTA |
1. 序列比对相关概念
|
两条长度为\(n\)的序列比对的排列组合: \( (2n)!/(n!)^2 \) 设n=300, \((2*300)!/(300!)^2 \approx 7*10^{88} \) 目前可见宇宙中所有原子的一亿倍! |
1. 序列比对相关概念
|
ATGACTGGA
||||||||| ATGACTGGA |
ATGA--CTGGA
|||| ||.|| ATGATGCTCGA |
|
|
|
1. 序列比对相关概念
|
1. 序列比对相关概念
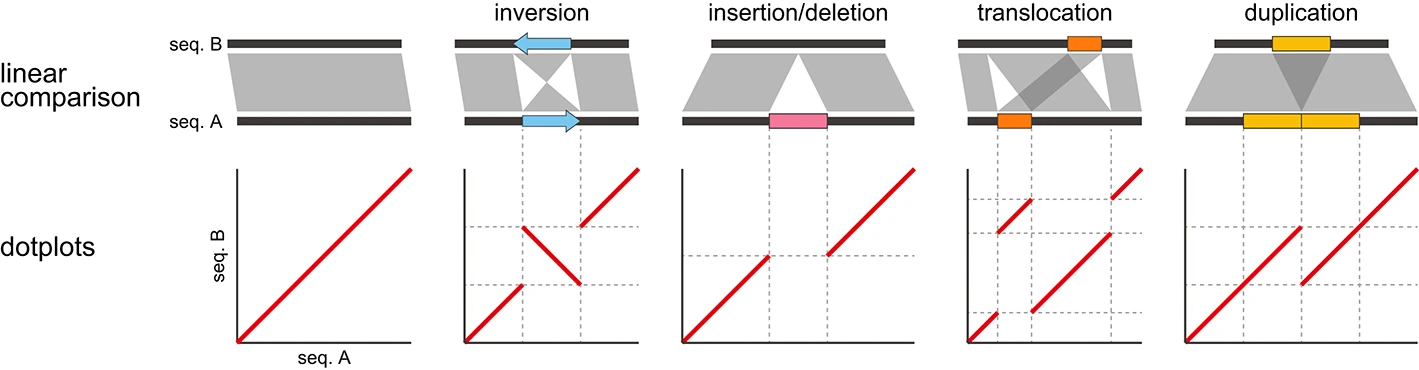
1. 序列比对相关概念
1. 序列比对相关概念
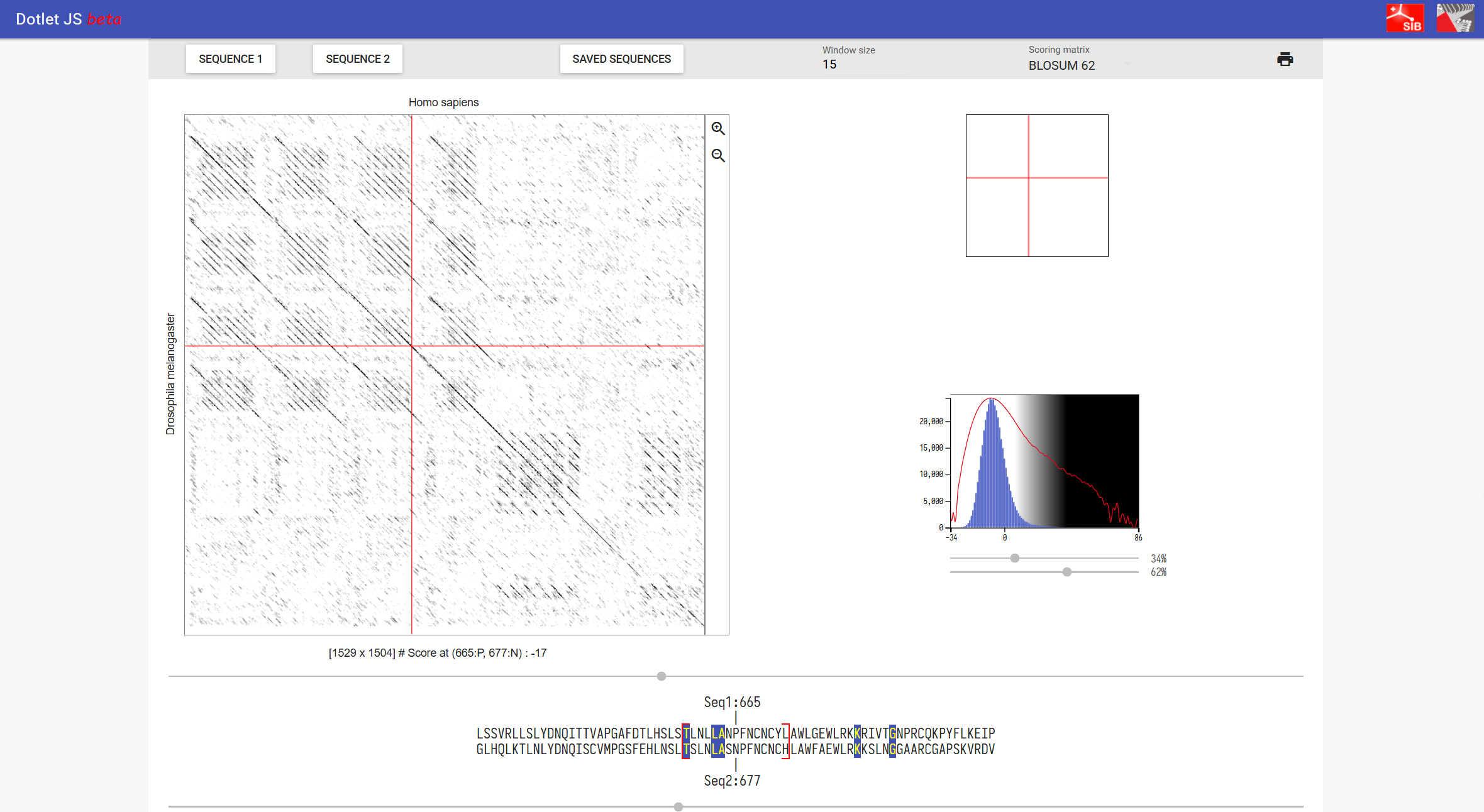
1. 序列比对相关概念
|
AGCACCACCA |........| ACACGATCTA |
AGCACCACC-A | |||.|.| | A-CACGATCTA |
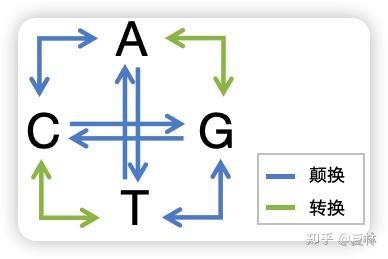 |
汉明距离(Hamming distance): 两个 字符串对应位置的不同字符的个数。(没有gap) 编辑距离(Edit distance, ): 将一个字符 串通过插入、删除、替代等操作变为另一个字符串的最少操作次数。 针对上述序列:
|
1. 序列比对相关概念
|
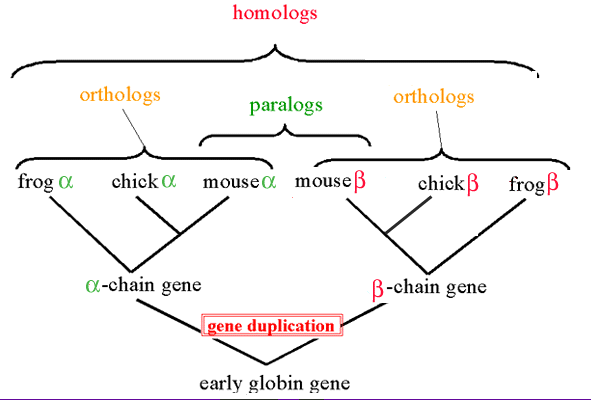
相似性和同一性都是量的概念,一般用百分数表示; 同源性是质的判断, 要么同源要么不同源。 |
直系同源基因和旁系同源基因统称为同源基因(homolog) |
1. 序列比对相关概念
生物信息学
序列比对: 2. 打分矩阵
桂松涛 Blog
songtaogui@163.com

2025年09月
2. 序列比对打分方法
|
|
2. 序列比对打分方法
2. 序列比对打分方法
|
|
2. 序列比对打分方法
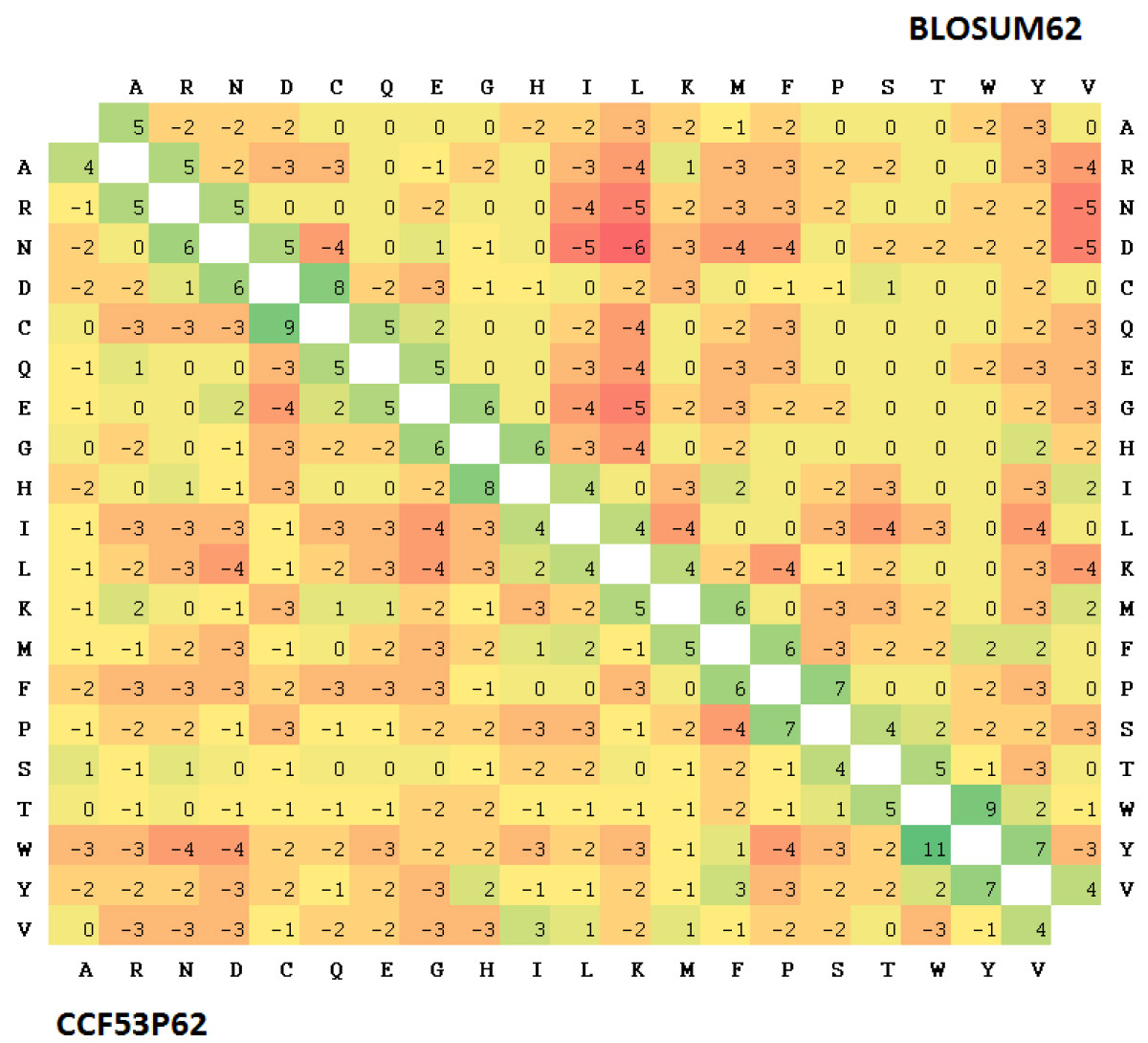 |
2. 序列比对打分方法
|
PAM
|
BLOSUM
|
2. 序列比对打分方法
|
ATGA--CTGGA |||| ||.|| ATGATGCTCGA
|

|
生物信息学
序列比对: 3. 比对算法
桂松涛 Blog
songtaogui@163.com

2025年09月
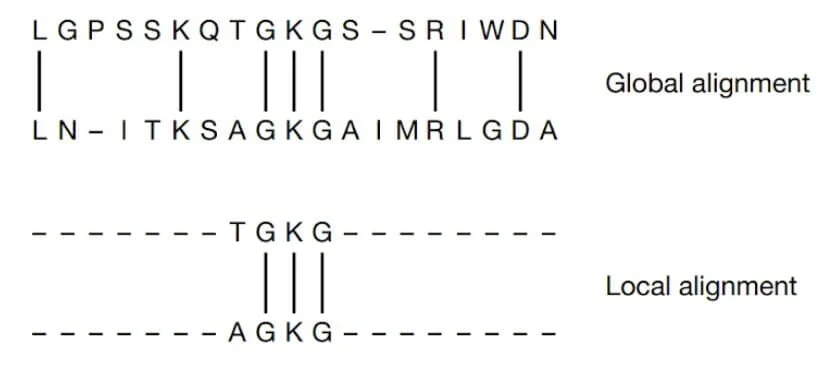
3. 比对算法

|
|
3. 双序列比对算法
|
|
|
3. 双序列比对算法
3. 双序列比对算法
3. 双序列比对算法
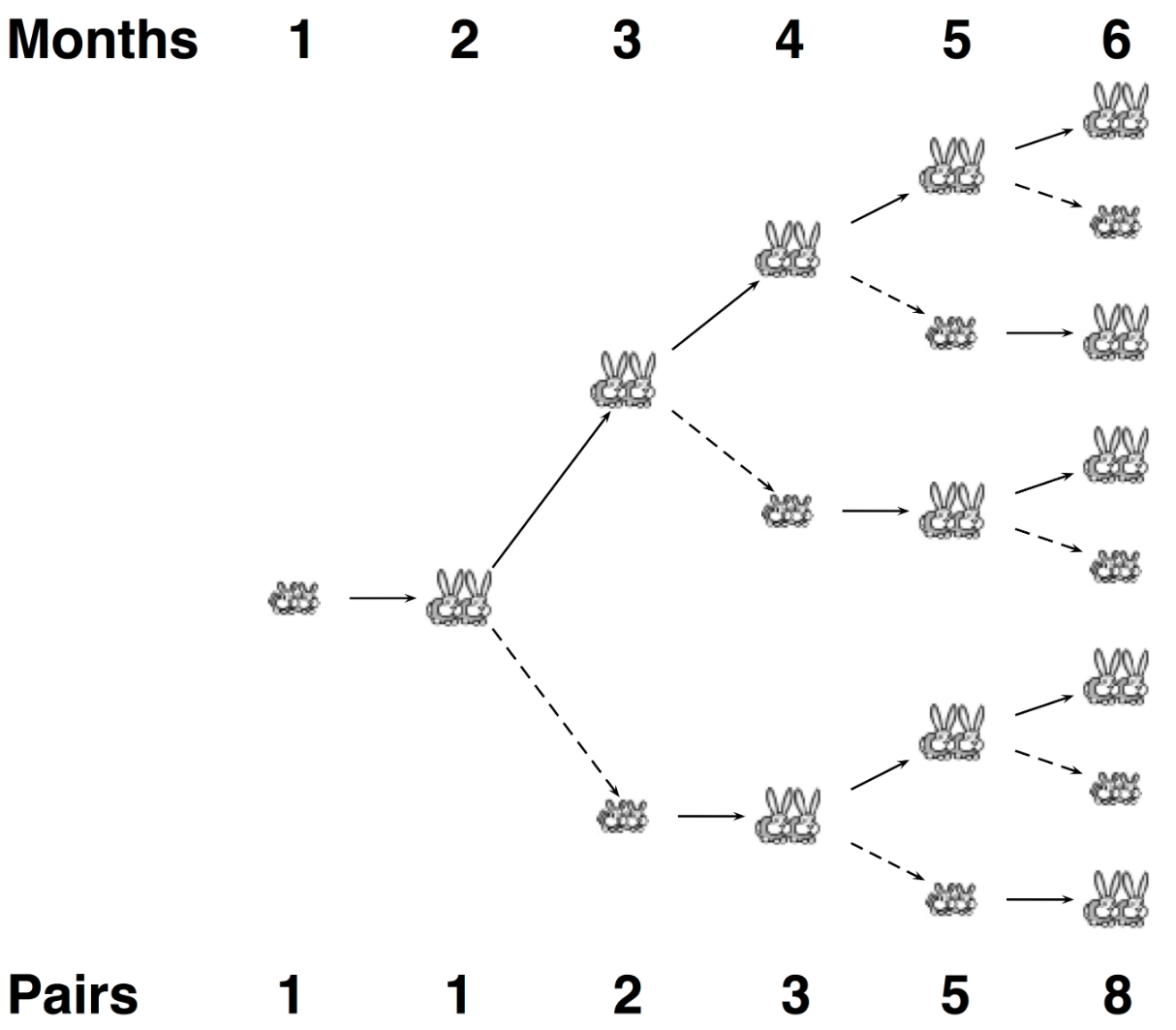 |
递归思路的解决方案: 递归会带来大量的重复计算 |
3. 双序列比对算法
|
递归思路的解决方案: |
动态规划的解决方案: |
3. 双序列比对算法
3. 双序列比对算法
|
|
|
3. 双序列比对算法
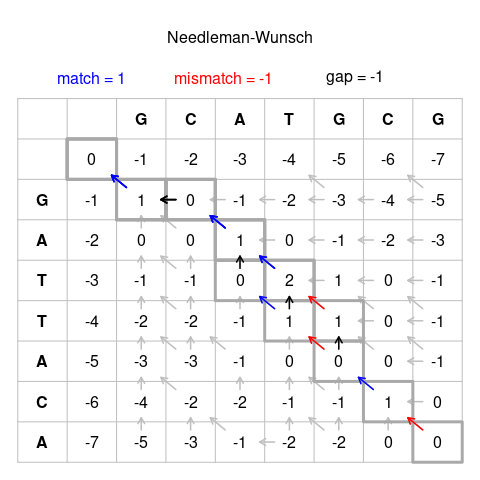
3. 双序列比对算法
3. 双序列比对算法
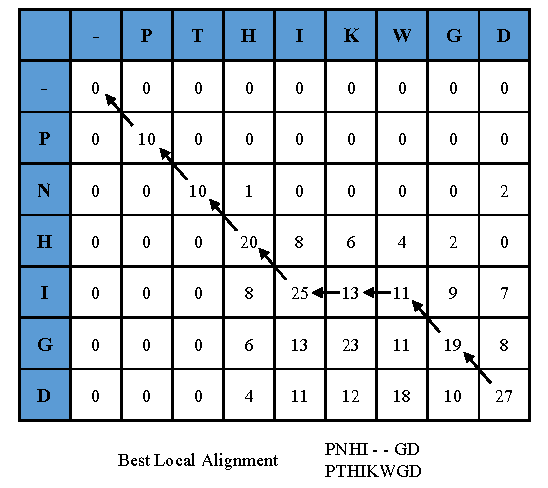
|
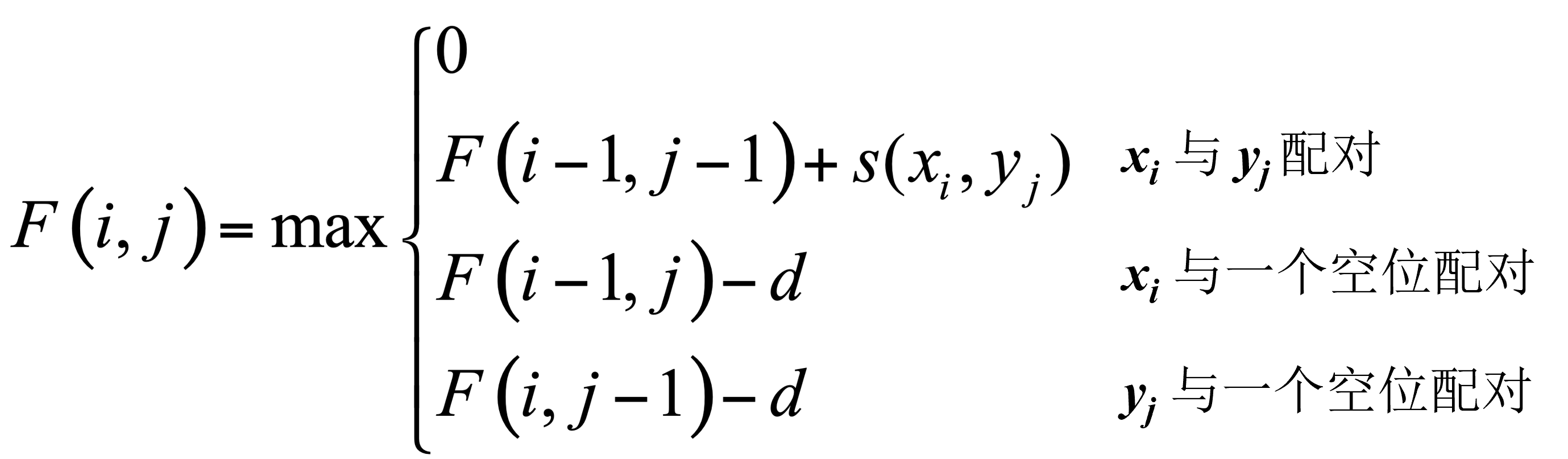
|
3. 双序列比对算法
3. 双序列比对算法
3. 双序列比对算法
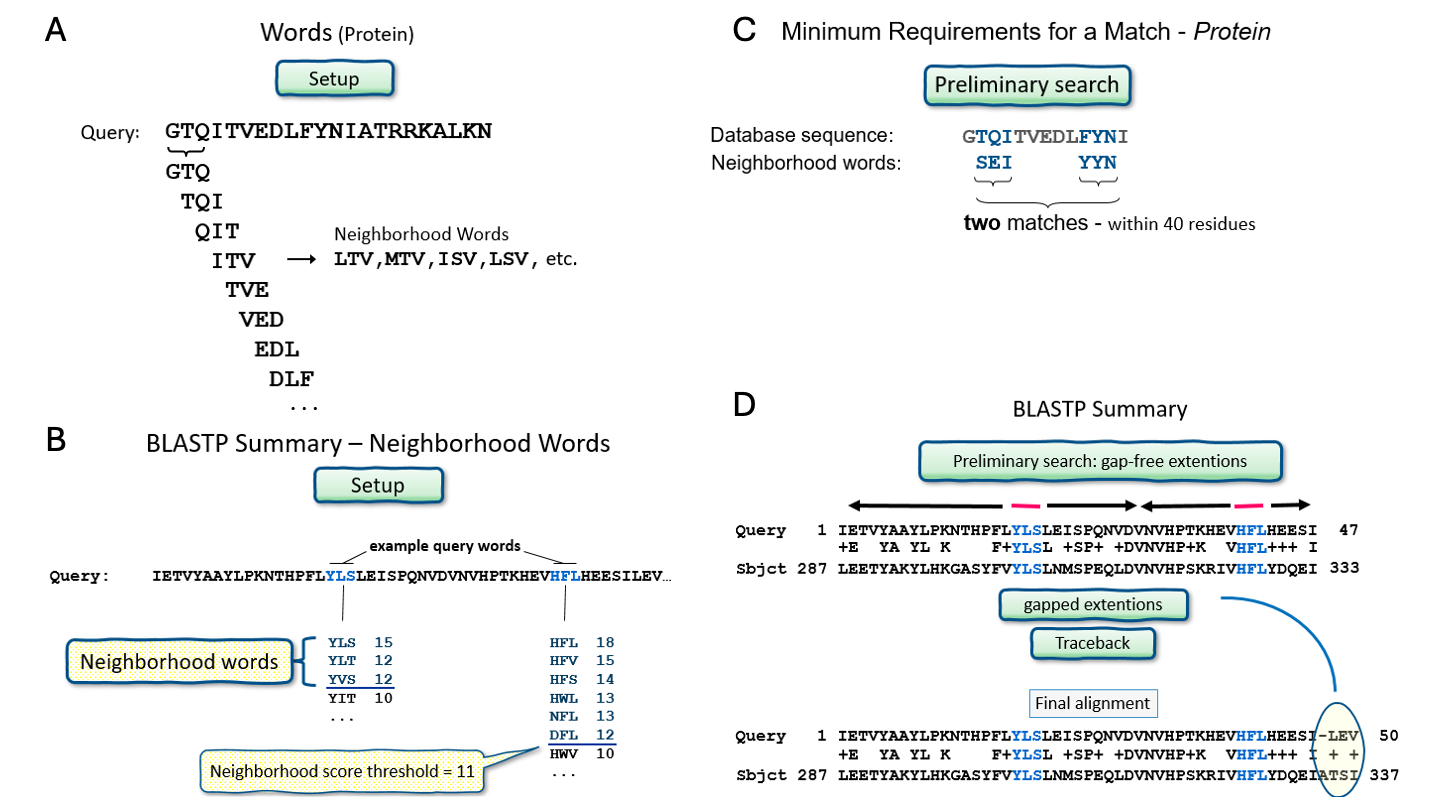
3. 双序列比对算法

3. 双序列比对算法
|
|

|
3. 双序列比对算法
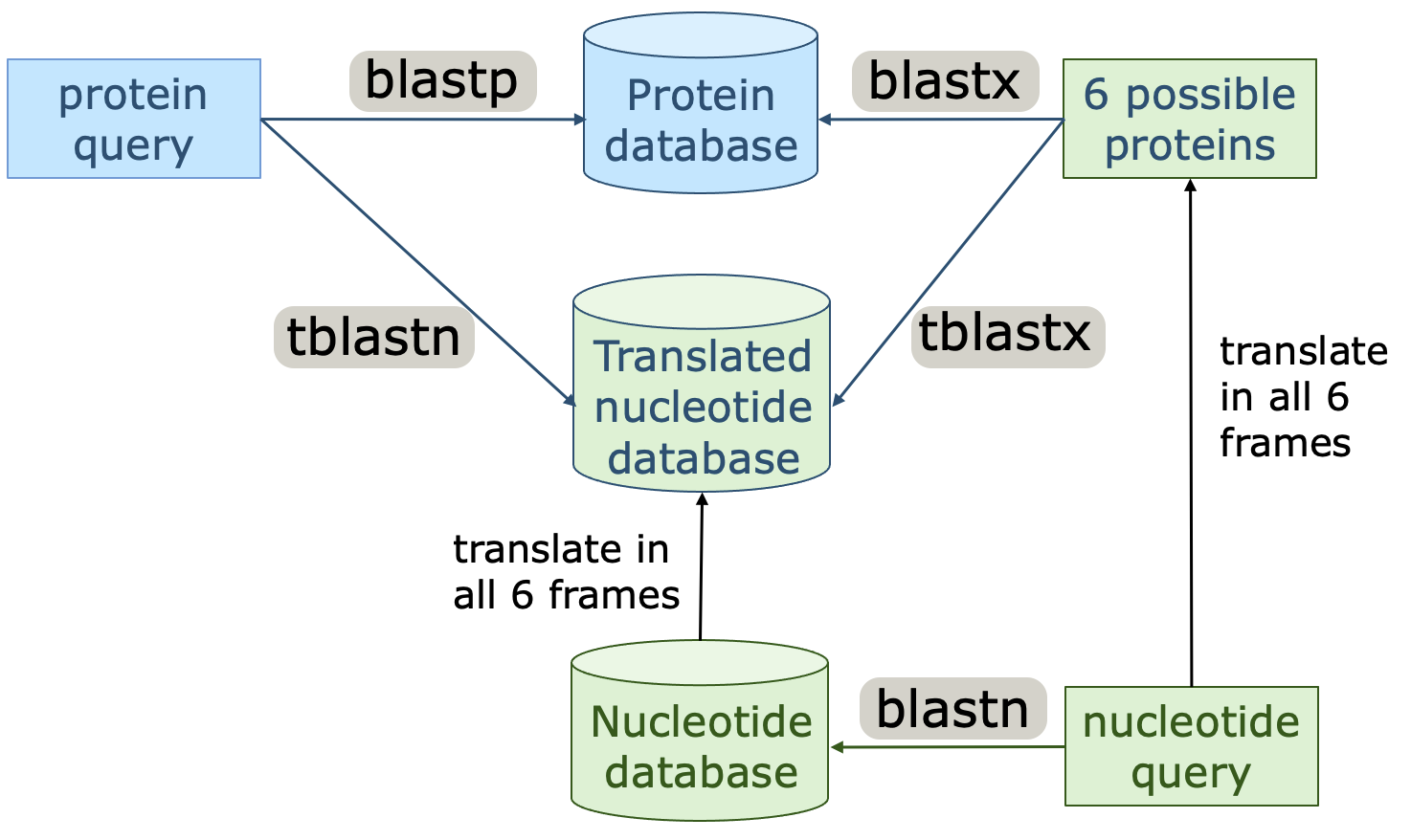
生物信息学
序列比对: 4. 多序列比对
桂松涛 Blog
songtaogui@163.com

2025年09月
4. 多序列比对
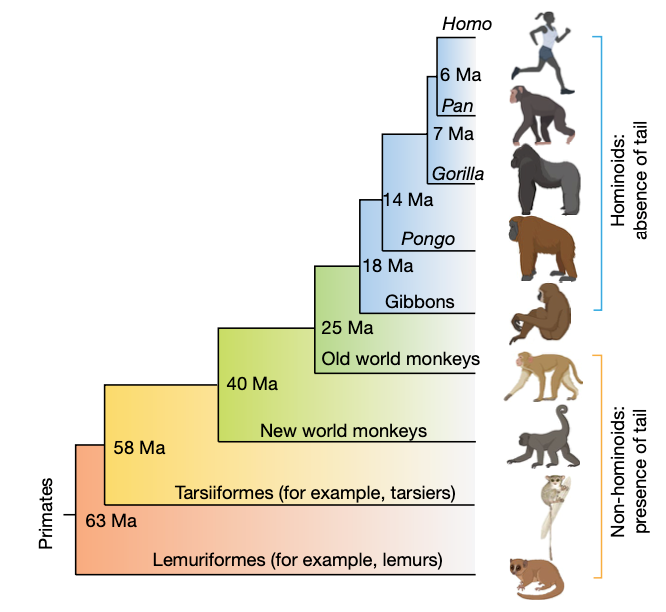 |
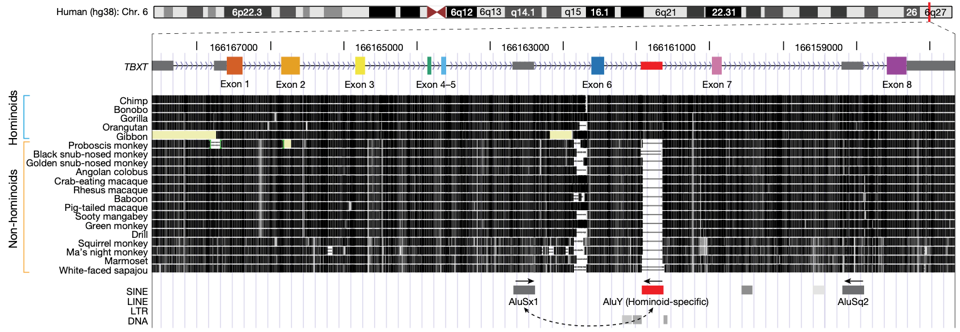 |
4. 多序列比对
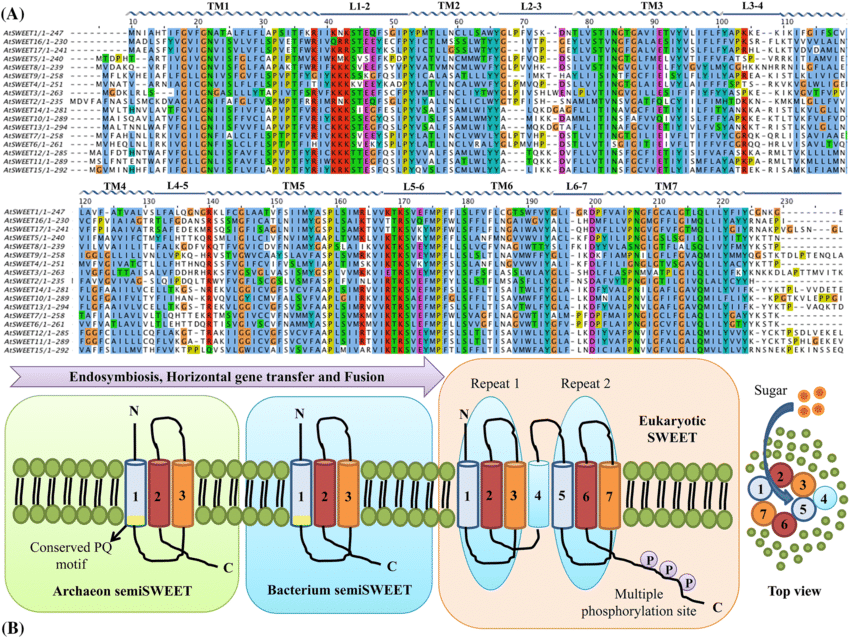
4. 多序列比对
4. 多序列比对
|
|

|
4. 多序列比对
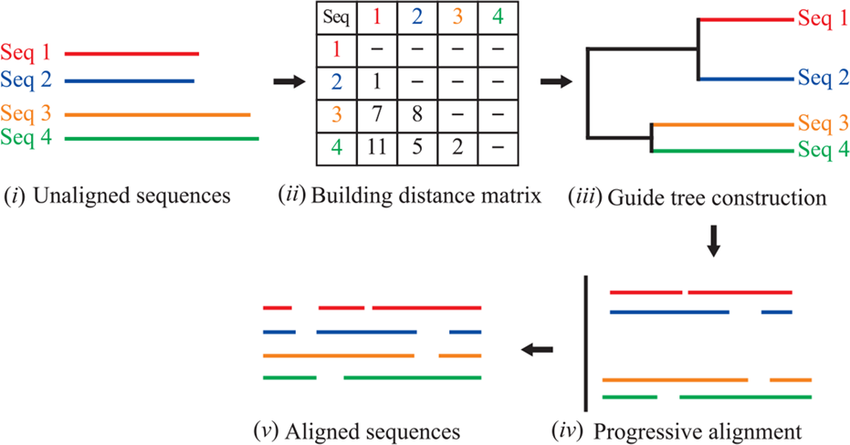
4. 多序列比对
Clustal Omega

推荐资料